kivantium活動日記

プログラムを使っていろいろやります

DRV8825でNEMA 17ステッピングモーターを回す

DRV8825というモータードライバーを使ってNEMA 17ステッピングモーターを回してみた。 だいたいStepper Motor with DRV8825 and Arduino Tutorial (4 Examples)を読めば分かるのだが、まとまった日本語文献が見当たらなかったので書き残しておく。

部品について

ステッピングモーターは3Dプリンターのような正確な位置決めが必要になる用途で使われる。 モーターを回すには比較的大電流が必要になるため、モータードライバーと呼ばれるICを使うことが一般的である。 今回は比較的安価で評判の良かったDRV8825を使うことにした。 ICをそのまま使うのは面倒なので各種部品を追加したモジュールがPololu社から販売されており (Pololu - DRV8825 Stepper Motor Driver Carrier, High Current)、その互換品をAmazonで購入した。

ステッピングモーターにはいろいろ種類があるのだが、今回はよく使われるNEMA 17という種類のものを使うことにする。 NEMA 17はNational Electrical Manufactures Associationが定めた規格で、大きさが 1.7 x 1.7 inch (42.3 x 42.3 mm) であることが決まっている。 それ以外に何が定められているのかはよく知らないのだが、NEMA 17準拠を謳うモーターでも高さや電圧にはバラつきがあるので割と緩い規格のようだ。 NEMA 17に準拠したモーターの例は https://reprap.org/wiki/NEMA_17_Stepper_motor などに挙げられている。 今回は電圧12V・高さ39mmの17HS15-1504S-X1というモーターをAmazonで購入した。

モーターを制御するArduinoなどを含めた買い物リストは以下の通りである。

買い物リスト

ハードウェアの設定

電流制限の設定

今回購入したモジュールはポテンショメータを回すことで電流制限の調整を行うことができる。このモジュールは最大で2.5Aしか流せないのだが、初期位置によってはそれよりも多い電流が流れる設定になっている場合があるのでモーターをつなぐ前に設定値を確認する必要がある。ブレッドボードを用いて以下のような回路を組む。

最大電流設定の回路。MakerguidesからCC BY-NC-SA 4.0ライセンスに基づき掲載。

右上の電源にはモーター用の電源12Vをつなぐ。ドライバーでポテンショメータを回して、GNDとポテンショメータ間の電圧を測定することで電流値を設定できる。ポテンショメータの電圧をVref (V)とすると 最大電流 (A) = Vref x 2 という関係が成り立つ。このモジュールはヒートシンクなしで1.5Aまで流せるので、とりあえず0.75 Vくらいに設定するのが良いだろう。

Vrefの測定方法。MakerguidesからCC BY-NC-SA 4.0ライセンスに基づき掲載。

設定方法についての公式動画はここに上がっている。 www.youtube.com

解説

最大電流 (A) = Vref x 2 という公式だが、左右で単位が揃っていなくて気持ちが悪い。DRV8825のデータシートに掲載されている元の数式は I_{\text{CHOP}} = \frac{V_{(\text{xREF})}}{5 \times R_{\text{ISENSE}}} というものである。ここでモータードライバモジュールの回路図を確認するとR_{\text{ISENSE}}は0.1 Ωなので、最大電流 (A) = Vref (V) / 0.5 (Ω) がこの公式の本来の姿となる。

モーターの配線

最大電流を設定できたらいよいよモーターの配線を行う。次のように接続すればよい。

モーターの配線。MakerguidesからCC BY-NC-SA 4.0ライセンスに基づき掲載。

モーターから出るケーブルの色は型番によって異なるようなのだが、とりあえず左から順番につないでおけば動いた。一応解説しておくと、このモジュールのピン配置は以下のようになっている（モジュールを裏返すと書いてある）。

ピン配置。MakerguidesからCC BY-NC-SA 4.0ライセンスに基づき掲載。

  • VMOT: モーター用電源の+端子を接続する
  • GND: 片方はモーター用電源の-端子に、もう片方はArduinoのGNDに接続する
  • SLP・RST: Arduinoからの5Vに接続する
  • DIR: Arduinoの2ピン
  • STP: Arduinoの3ピン

接続が完了したらArduinoに以下のコードを書きこむ。なお、配線が間違っていた場合にPCのUSB端子に12Vが掛かってダメージを受けるのを防ぐため、私はいつも電源を外した状態でプログラムを書き込み、その後ArduinoをPCから外して外部電源につなぎなおしてから12V電源をつなぐようにしている。

/* Example sketch to control a stepper motor with 
   A4988/DRV8825 stepper motor driver and 
   Arduino without a library. 
   More info: https://www.makerguides.com */

// Define stepper motor connections and steps per revolution:
#define dirPin 2
#define stepPin 3
#define stepsPerRevolution 200

void setup() {
  // Declare pins as output:
  pinMode(stepPin, OUTPUT);
  pinMode(dirPin, OUTPUT);
}

void loop() {
  // Set the spinning direction clockwise:
  digitalWrite(dirPin, HIGH);

  // Spin the stepper motor 1 revolution slowly:
  for (int i = 0; i < stepsPerRevolution; i++) {
    // These four lines result in 1 step:
    digitalWrite(stepPin, HIGH);
    delayMicroseconds(2000);
    digitalWrite(stepPin, LOW);
    delayMicroseconds(2000);
  }

  delay(1000);

  // Set the spinning direction counterclockwise:
  digitalWrite(dirPin, LOW);

  // Spin the stepper motor 1 revolution quickly:
  for (int i = 0; i < stepsPerRevolution; i++) {
    // These four lines result in 1 step:
    digitalWrite(stepPin, HIGH);
    delayMicroseconds(1000);
    digitalWrite(stepPin, LOW);
    delayMicroseconds(1000);
  }

  delay(1000);

  // Set the spinning direction clockwise:
  digitalWrite(dirPin, HIGH);

  // Spin the stepper motor 5 revolutions fast:
  for (int i = 0; i < 5 * stepsPerRevolution; i++) {
    // These four lines result in 1 step:
    digitalWrite(stepPin, HIGH);
    delayMicroseconds(500);
    digitalWrite(stepPin, LOW);
    delayMicroseconds(500);
  }

  delay(1000);

  // Set the spinning direction counterclockwise:
  digitalWrite(dirPin, LOW);

  //Spin the stepper motor 5 revolutions fast:
  for (int i = 0; i < 5 * stepsPerRevolution; i++) {
    // These four lines result in 1 step:
    digitalWrite(stepPin, HIGH);
    delayMicroseconds(500);
    digitalWrite(stepPin, LOW);
    delayMicroseconds(500);
  }

  delay(1000);
}

プログラムはMakerguidesからCC BY-NC-SA 4.0ライセンスに基づき掲載。

正しく設定できていればモーターが左右に回転するはずである。

ここまでできれば、あとはAccelStepperライブラリやStepperDriverライブラリなどでステッピングモーターを制御できるはずである。既に文献がありそうなのでここでは割愛する。 また、ブレッドボードで大電流を流すのは推奨できないのでこの構成はあくまでテスト用であり、本番実装では適切な配線を行うべきである。

docxファイルに埋め込まれたPDFを読む方法

論文を読んでいたらsupplementary materialとして提供されたdocxファイルの中にPDFが埋め込まれていた。本来はダブルクリックすると開けるはずなのだが、どうしても開くことができず困ったので解決策をメモしておく。

結論

  • 1: docxファイルのファイル名を変更して拡張子をzipに変更する。
  • 2: zipファイルを解凍するなどして word/embeddings 内にある oleObject1.bin を取り出す。（数字は異なる場合がある）
  • 3: WSLなどのPython環境で以下のスクリプトを実行する。
import os

str1 = b'%PDF-'  # Begin PDF
str2 = b'%%EOF'  # End PDF

with open('oleObject1.bin', 'rb') as f:
    binary_data = f.read()

# Convert BYTE to BYTEARRAY
binary_byte_array = bytearray(binary_data)

# Find where PDF begins
result1 = binary_byte_array.find(str1)

# Remove all characters before PDF begins
del binary_byte_array[:result1]

# Find where PDF ends
result2 = binary_byte_array.find(str2)

# Subtract the length of the array from the position of where PDF ends (add 5 for %%OEF characters)
# and delete that many characters from end of array
to_remove = len(binary_byte_array) - (result2 + 5)

del binary_byte_array[-to_remove:]

with open(os.path.expanduser('test1.pdf'), 'wb') as fout:
    fout.write(binary_byte_array)
  • 4: 出力された test1.pdf をお好みのPDFリーダーで読む。

この方法は原理的にはxlsxファイルやpptxファイルにも使えるはずである。

ネタ元→ python 3.x - How can I decode a .bin into a .pdf - Stack Overflow

試したが失敗した方法

  • Word内で埋め込みPDFをダブルクリックするのが正当な開き方なのだが、

このオブジェクトは Acrobat で作成されましたが、このプログラムがお使いのコンピューターにインストールされていないか、応答していません。このオブジェクトを編集するには、Acrobat をインストールするか、Acrobat でダイアログ ボックスが開いていないことを確認します。

というエラーで開くことができなかった。

Pythonを使う方法は一般ユーザー向けではない最後の手段という感じがするので、もう少しユーザーフレンドリーな方法を考えたいところである……。

創作+機械学習 Advent Calendar 2022 結果発表

昨年末に創作+機械学習 Advent Calendar 2022を開催しました。 今年は13記事の投稿がありました。ご参加いただいた皆様ありがとうございました。

kivantium.hateblo.jp

優秀賞の発表

記事を投稿していただいた10名を対象に1/3〜1/10の期間で投票を行いました。 主催者の記事を除く7本の記事の記事の中から、良いと思った記事に1人3票投票していていただきました。投票へのご協力ありがとうございました。

受賞対象の記事は以下の通りです。

最優秀賞

優秀賞

佳作

最優秀賞には2万円、優秀賞には1万円、佳作には5000円が授与されます。 3位までを優秀賞とする予定でしたが、3位の得票数が同じだったため優秀賞の賞金を二分して佳作という扱いにしました。

また、今回は参加者が少なかったため審査員特別賞の代わりに参加者全員に参加賞を授与することにしました。参加賞の賞金は2000円です。 受賞者の皆様には近日中に賞金の受け取り方法について個別に連絡します。

受賞者の皆様（画像は@yumu_7さんに作っていただきました。イラスト制作は@tesimeneさんです）

全体所感（midzさん）

今回は前回と比べると、「モデルを構築した話」よりは、「既存の機械学習サービスをどのように創作に応用するかの方法論」の方が全体的に多かったように感じられます。

特にテキストから画像を生成するサービスが次々と登場し、情勢を追うだけでも大変になった年であったように感じます。

創作に機械学習を応用することが当たり前になる時代に突入しつつあり、そのこと自体は良いことですが、開発競争が激化したために、個人開発で行えることの余地が少なくなってしまったデメリットもあるように感じます。

最優秀賞のLWさんは、機械学習で生成した絵を小説の挿絵として使う方法論を紹介してくださいました。現状制御が難しい画像生成AIを応用する上での妥協点をどう探るべきかを詳しく書いてくださっています。

優秀賞のBrightWaltzさんは、実際に作曲や音楽演奏をしていらっしゃる立場から、音楽生成AIの即興演奏への応用方法を１．AI先行、人後攻、２．人先行、AI後攻、３．AIと人によるリアルタイムインタラクティブ演奏という３つの観点から試した例をご紹介いただきました。

このように、創作をAIに応用することが現実的に可能になった段階では、それぞれの分野のドメイン知識、創作経験が重要だと感じさせてくれた記事であったと思います。

2022年夏頃から一気に創作AIのサービス化競争が熾烈になりました。これまでにAIはブラックボックスだからだめだと散々言われてきましたが、AIが高性能化していくと、人がむしろAIに合わせるような方法を考え出すようになったのが興味深い点でした。これからも創作AIは発展を続けると思いますが、人がAIに寄るのか、AIが人に寄ってくるのか、今後の展開にも目が話せません。今年の年末も楽しみです。

宣伝

このAdvent Calenderは2dmlというDiscordサーバーで企画・運営されました。このサーバーでは創作と機械学習に関する情報交換やイベントの開催を行っています。興味がある方は是非ご参加ください。

招待リンク: https://discord.gg/jQNXjkrqGU

以上です。創作+機械学習 Advent Calendar 2022 にご参加いただいた皆様ありがとうございました。2023年もよろしくお願いします。

姿勢推定を用いたキャラクター画像検索

この記事は創作+機械学習 Advent Calendar 2022の1日目です。

adventar.org

はじめに

去年のAdvent Calendarから一年が経ち、再びAdvent Calendarの季節がやってきました。毎年のことながら時間が流れるのは早いものです。

2022年には拡散モデルを用いた画像生成AIが大発展を遂げました。2015年に話題となったDCGANによるアニメ画像生成（抹茶さんのツイート・rezoolabさんの記事）とNovelAIの生成画像（pixivをNovelAIで検索した結果）を比較すると、まさに隔世の感があります。AIのべりすとをはじめとする言語モデルの応用も進み、小説投稿サイトでAI支援を利用して生成された小説を見かけることも珍しくなくなってきました。

生成モデルが進展した一方、今年は機械学習の訓練データの扱いを巡る論争が激化した年でもありました。mimicの炎上は記憶に新しいところです。海外ではGoogle Copilotに対する集団訴訟が提起されています。

機械学習の創作への応用が正と負の両面で盛り上がった2022年でした。そんな今年のAdvent Calendarにどのような記事が投稿されるのか楽しみにしています。スペースにはまだまだ空きがありますので興味を持った方は今からでも是非登録してみてください。

姿勢推定を用いたキャラクター画像検索

この記事では姿勢推定を用いたキャラクター画像検索サービスについて紹介します。

絵を描く際に類似ポーズのイラストを参考にすることがありますが、イラストをポーズで検索することは難しく、せいぜい「手を上げる イラスト」のようなキーワードで検索することしかできないのが現状です。また、NovelAIが登場した当初、生成画像が学習データに酷似しており、学習データの姿勢を保存して画風を変換するような仕組みになっているのではという疑惑の声が上がっていました。学習元のデータセットから姿勢が似ている画像を検索することができれば学習データとの類似性を判定できる可能性があります。（なお現在はStable Diffusionに独自の改造を施したものであることが判明しています: 公式解説）

そこで、姿勢推定を用いてキャラクター画像を検索できるサービスを開発することにしました。

実装

姿勢推定アルゴリズムにはbizarre-pose-estimatorを利用しています。

このモデルは入力画像に対して25個の特徴点（17個のCOCO keypointsと8個の中間点）を返します。

COCO keypoints と中間点（画像はKhungurn, et al からの引用）

元論文によると検索対象のデータセットは以下のように構築されています。

  1. 検索対象の各キャラクターを囲むバウンディングボックスと25個の特徴点を求める
  2. 特徴点をバウンディングボックスの長辺の長さで正規化する
  3. 正規化された各特徴点間のユークリッド距離を保存する

正規化された特徴点間の距離を利用することで、並進・回転・拡大・縮小に対して不変の特徴量を得ることができます。特徴点は25個あるので _{25} C_2 =300次元ベクトルになります。

Hugging Faceへのデプロイ

このモデルはメモリの消費量が多いため、手持ちのサーバーにデプロイすることができませんでした。そこで、Hugging Face上にアプリを構築しました。

huggingface.co

このアプリではアップロードされた画像の姿勢に類似したの画像を検索することができます。現在は元論文のレポジトリに付属していたデータセットを検索対象としています。このデータセットはDanbooru上でfull_bodyタグがついた単一キャラクターの画像からなるそうです。

にじさーちへの組み込み （β版）

また、このモデルを利用したポーズ検索機能を我々が開発している画像検索サイトのにじさーちに試験的に実装しています。メモリ容量の関係でアップロード画像の姿勢を推定することができないため、代わりに棒人間を動かして検索するユーザーインターフェースを採用しました。検索対象が6000枚程度なので検索性能はあまりよくありません。 （フロントエンドの実装は@amane_lyricに協力していただきました）

ポーズ検索の例 (https://nijisearch.kivantium.ai/pose_search/)

開発に興味のある方は是非pull requestを送ってください。

github.com

今後の課題

現在利用しているモデルは全身画像を前提としているため、全身が写っていない画像の姿勢推定を行うことができません。投稿されるイラストの多くは身体の一部が写っていないため、検索対象にできる画像の枚数が限られてしまいます。

また、特徴点間のユークリッド距離を特徴量として用いているためか、検索結果が直感的にいまいち正しくないと感じることが多くあります。人間がより自然に感じる姿勢類似性の基準を考える必要がありそうです。

宣伝

私達が発行している同人誌 Pythia 2.0 に『画像からのアニメキャラクター姿勢推定』という記事が掲載されています。

thetenthart.booth.pm

創作+機械学習 Advent Calendar 2022 を開催します

創作+機械学習 Advent Calendar は参加者の皆様に創作（漫画・アニメ・イラスト・小説・音楽・ゲーム等）と機械学習に関連した記事を投稿していただき、優れた記事を書いた方に賞を贈呈する企画です。

この企画は去年に引き続いての開催となります（去年の告知記事と結果発表）。

告知画像（@yumu_7さんに作っていただきました。イラストは@tesimeneさんに描いていただいたものです）

ルール

  • 参加の意思表示はAdventarに記事公開日を登録することで行います。
  • 登録日になったら創作（小説、漫画、アニメ、イラスト、映画、音楽、ゲーム等）と機械学習または統計分析に関連する記事を公開してください。
  • 2022年内に記事を公開された方を賞の審査対象とします。記事の公開が年内であれば空き枠に後から登録した場合も審査対象になります。
  • 一人で複数の記事を投稿しても問題ありません。カレンダーの枠が埋まった場合は2枚目を作成します。
  • 記事の公開が登録日よりも遅れる場合はその旨をAdventarに記載してください。コメントがないまま遅れた場合は主催側の判断で登録を解除する場合があります（その場合も後日再登録することが可能です）
  • 2023年1月に参加者の相互投票で優秀賞を決定します。
  • 賞に関する連絡を送る場合がありますので、2dml Discordに参加する・Twitterで@kivantiumからのダイレクトメッセージを受信できる状態にする（DM解放またはフォロー）・メールアドレスなどの連絡先を記事中に記載する等の方法で主催者と連絡が取れる状態にしてください。
  • 記事を投稿してくださった方にはコミケや技術書典等で出版する同人誌への投稿を後日依頼する可能性があります。

記事の書き方

  • 記事の形式は主にブログを想定していますが、動画やスライドなどでも大丈夫です。インターネット上で自由に閲覧できるものであれば形式は問いません。
  • 記事の冒頭に創作+機械学習 Advent Calendar 2022 の記事であることを明記してください。
  • 記事の言語は日本語または英語が望ましいです。
  • 推奨ハッシュタグは #創作機械学習 です

テーマの例

  • 画像関係: 画像分類・画像生成・自動着色・モーションキャプチャ・各種イラスト生成AIのテクニックなど
  • 言語関係: 小説生成・チャットボットなど
  • 音声関係: 音楽生成・音声合成・声質変換など
  • 統計分析: キャラクター分析・感情分析など
  • 創作支援: 機械学習による創作支援ツールの紹介・ツールに支援されて作った作品の紹介など
  • その他: データベースの作成・ゲームの自動プレイ・推薦システム・AIを創作に使用するための方法論など

具体的な記事例は去年のAdvent Calendarを参考にしてください。

上に挙げた以外のテーマでももちろん大丈夫です。カレンダーのタイトルは「機械学習」としていますが、実際には人工知能関連の技術を幅広く対象にします。何が人工知能技術なのかについては人工知能学会のAIマップを参考にしてください。

人工知能学会「AIマップβ 2.0 （2020年6月版）」 https://www.ai-gakkai.or.jp/resource/aimap/

未完成のものやアイデア段階の記事も歓迎します。「〜というデータを集めて、自動で〜する機械学習モデルを作りたいと思っています。協力者募集」みたいな感じでも問題ありません。

賞について

以下の賞を用意しています。審査員特別賞を提供してくださる方がいらっしゃったら連絡してください。

  • 最優秀賞 (1名) 賞金20000円
  • 優秀賞（2〜3名）賞金10000円
  • 佳作（若干名）
  • 審査員特別賞
    • @kivantium賞（機械学習の使い方に新しさを感じる記事を書いた方に授与）
    • @thetenthart賞（創作支援に役立ちそうな記事を書いた方に授与）
    • @xbar_usui賞（機械学習を知らない人でも楽しめる記事を書いた方に授与）

賞金はAmazonギフトカードでの支払いを予定していますが、希望があれば他の方法にも柔軟に対応します。 皆様の投稿をお待ちしております。

宣伝

Discordサーバー

創作と機械学習に関するDiscordサーバー 2dml があるので、興味がある方はご参加ください。このAdvent Calendarの運営についてもこのDiscordで議論しています

招待リンク: https://discord.gg/jQNXjkrqGU

discord.gg

同人誌

去年のAdvent Calendar参加者を中心に執筆した同人誌をBoothで販売しています。売上はAdvent Calendarの賞金として活用させていただきます。

thetenthart.booth.pm

LT会

2022年11月5日に創作AIをテーマにしたLT会を実施します。詳細はconnpassをご覧ください。

connpass.com

3Dプリンター KP3S を買った

最近研究室に導入された3Dプリンターを見ていたら私物の3Dプリンターが欲しくなったのでKingroonのKP3Sを購入しました。テスト印刷が無事に成功したのでここまでの記録を残しておきます。

機種選定

家庭用に販売されている3Dプリンターは熱溶解積層方式 (FDM) と光造形方式の二種類が主流です。

  • 熱溶解積層方式 ― 溶かした材料を積み重ねてプリントする方式。取扱いが比較的簡単らしい
  • 光造形方式 ― 液体樹脂に紫外線を当てて固める方式。精度が高く仕上がりもきれいだが、二次硬化や廃液処理が面倒らしい。

みっきーさんのPhoton Mono 4K 光造形3Dプリンターを導入したを読んで光造形方式のPhoton Mono 4Kを購入することも検討したのですが、廃液処理が面倒そうだったのでFDM方式の機種を選ぶことにしました。

ANYCUBIC Photon Mono 4K 3Dプリンター 光造形 6.23" モノクロム スクリーン付き アップグレード LCD レジン 3D プリンタ 高速 超高精度 印刷サイズ 165 x 132 x 80mm

ANYCUBIC Photon Mono 4K 3Dプリンター 光造形 6.23" モノクロム スクリーン付き アップグレード LCD レジン 3D プリンタ 高速 超高精度 印刷サイズ 165 x 132 x 80mm

  • ANYCUBIC
Amazon

FDM方式の低価格帯モデルではEnder 3の人気が高いようでしたが、レビューによると組み立てに時間が掛かり調整も難しいという評判でした。

Creality 3D Ender 3 3Dプリンター 最大印刷サイズ220x220x250mm 停電復旧機能 高精度 初心者/学校等向け DIY 3Dプリンタ 日本語説明書

Creality 3D Ender 3 3Dプリンター 最大印刷サイズ220x220x250mm 停電復旧機能 高精度 初心者/学校等向け DIY 3Dプリンタ 日本語説明書

  • Creality 3D
Amazon

他の機種を探して「3Dプリンター 家庭用 おすすめ」などと検索してみたところ、KP3Sという機種が見つかりました。KP3Sは組み立てが簡単という評判で、日本語圏のユーザーも比較的多くいるようでした。特にKINGROON KP3S INFOというページにたくさんの情報が掲載されていたのが安心材料になり、購入を決定しました。

3Dプリンタープレミアムタイタン押出機アルミニウムダブルリニアガイドレール印刷スペース180x180x180mm

3Dプリンタープレミアムタイタン押出機アルミニウムダブルリニアガイドレール印刷スペース180x180x180mm

  • Kingroon
Amazon

開封の儀

Amazonで注文しました。

箱（側面に天地無用マークが書いてあったのにラベルが下面に貼られていたので上下逆さまの状態で届いた）

開封直後の状態。説明書などが入っている。

説明書などを取り出した状態。

箱から取り出した状態。プレートの文字が反対向きなので不安になるが、磁石でくっついているだけなのですぐに直せる。アームがちょっと重いので取り出すときには注意が必要。床を傷つけないようにダンボールなどを敷いてから作業に入った方が良かった。

組み立て

組み立てが簡単という前評判の通り、マニュアルは1ページだけでした。

組み立てマニュアル。英語版5ページより引用。

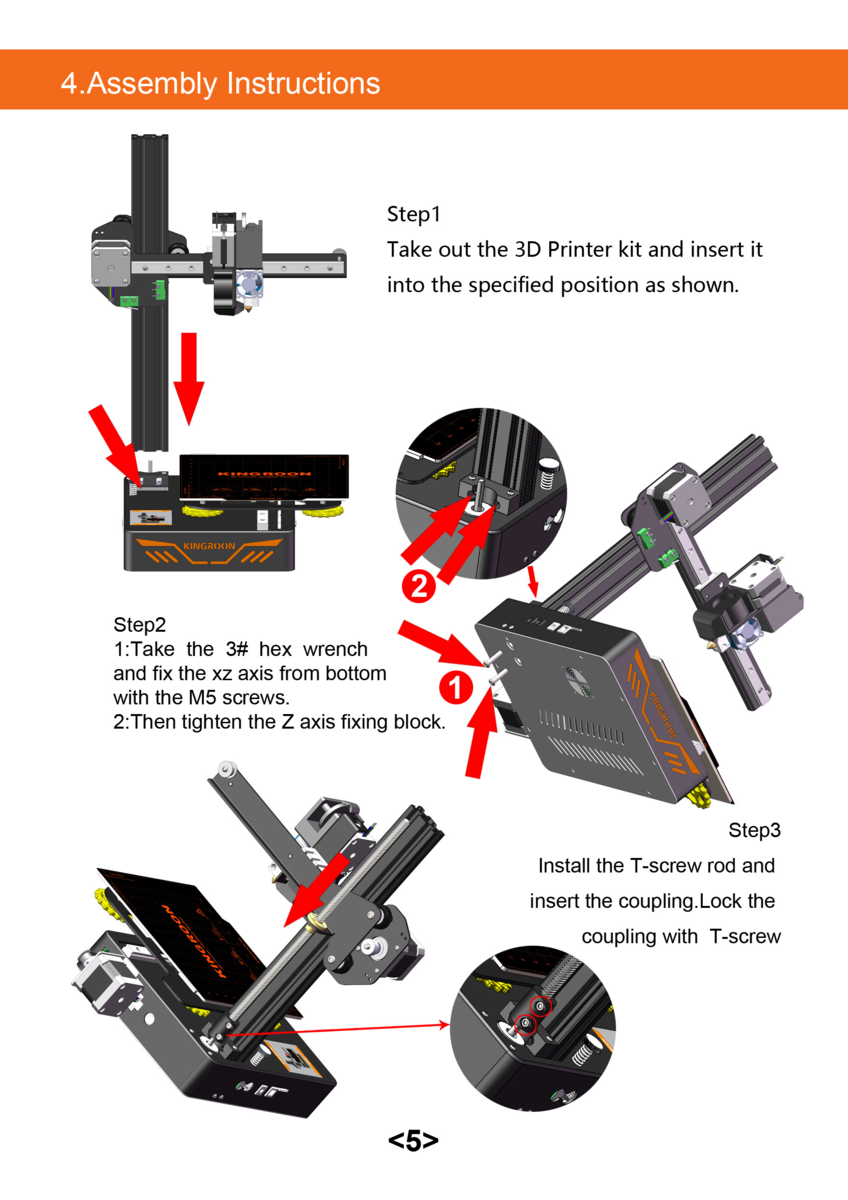
先人たちのブログに「組み立ては簡単で特に書くことがない」などと書いてあったので特に何も見ずに組み立てようとしたのですが、Step 2-2の "Then tighten the Z axis fixing block" を具体的にどうすればいいのか分からずそこで詰まってしまいました。"Z axis Screw" と書かれた袋にはネジと角型のナットのようなものが入っているのですが、図を見てもナットが書かれていないのです。

検索して出てきたFraxinus 01 - KINGROON KP3Sを購入してみた - まず分解。の説明に従って、Step 1の前にネジでナットを留めておき、その上からZ軸を差し込みました。

仮留めしたナット。この時点では緩めにしておく必要がある。

裏からZ軸を固定したところ。説明書の向きに倒すとノズルがX軸方向に動いてしまうのでこの方向に倒したほうが安定する気がする。

このZ軸固定方法は分かりにくいので他のブログで言及されていても良さそうなものですが、海外の動画などを見ても先ほどのブログ以外の言及が見当たりませんでした。状況証拠からすると、この角型ナットは古いバージョンでは存在しないんだと思います。

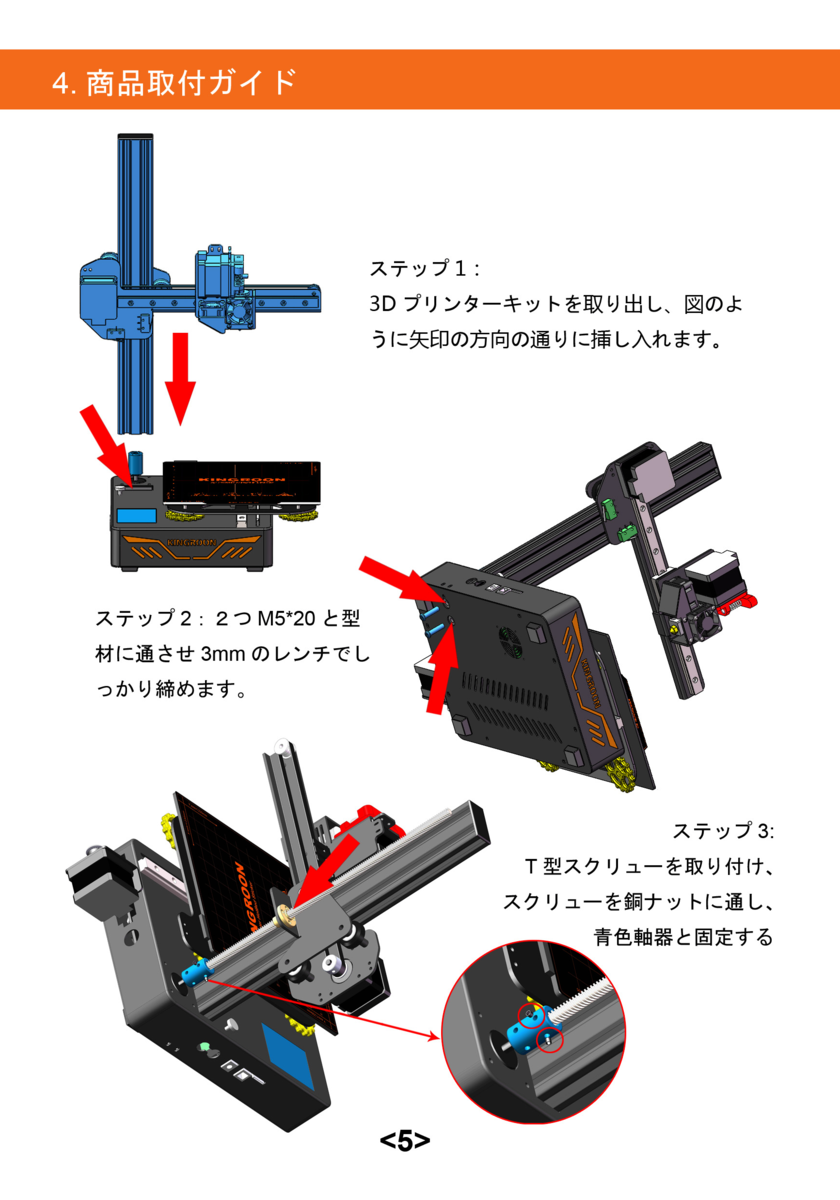
付属のSDカードに入っていた日本語版の組み立てマニュアルにはStep2-2がない。

公式の動画でも言及がありません。

www.youtube.com

ちなみに、この動画ではマニュアルに書いてないことも説明されているので組み立てる前に一度見ておいたほうがいいです。ノズルがプレートを傷つけないようにスポンジで挟んでおくことや電源の電圧設定スイッチはマニュアルに書いてあるべきだと思います。私は電源を入れた後にこの動画の存在に気がつきました。

あとはZ軸方向にT-screwを取り付けて電源をつなげば完成です。3ピンコンセントが必要なので注意してください。

完成図

レベリング

テスト印刷の前にノズルの位置を正しく設定するレベリング作業を行う必要があります。ノズルがプレートから0.1〜0.2mmの位置に来るように底面の高さを設定してやります。

レベリングは 激安３Dプリンタ Kingroon KP3Sを購入した（後編） - PikaPikaLightと基本的な使い方 – KINGROON KP3S情報を参考にしました。上に貼った公式動画にも説明があります。

大まかな手順は以下の通りです。

  • コピー用紙をプレートの上に置いておく
  • 本体の Leveling ボタンを押してノズルを所定の位置に移動させる
  • 隙間が空いている場合は本体左側の銀色のネジ (Z leveling Nut) を回して高さを大まかに調整する（このとき Move ボタンでノズルを上げる必要がある。ネジはコインを使うと回しやすい）
  • 再び Leveling ボタンを押して今度はプレート下側の黄色いネジで四隅の高さを調整する（黄色いネジは最初締めておき後から緩めるようにするとやりやすい）
  • コピー用紙を動かすときに抵抗を感じるが動かせないほどではない高さになったらOK（公式動画によれば "The proper distance between the nozzle and the hot bed is: A4 paper can be drawn out, and the paper cannot be pushed in. And there are no scratches on the paper." らしいですが、紙に線が残るかどうかギリギリのところまで狭めたほうが良かったです）

テスト印刷

レベリングが終わったらノズルを予熱し、付属のフィラメントを上の穴から差し込みます。最初はうまく入りませんでしたが、気合いで押し込んでいくとなんとか入りました。白いフィラメントを差し込んでいるのに青い糸状のものが出てきてびっくりしましたが、これは出荷時のテスト印刷に使われたものだと思われます。

フィラメントの挿入が終わったら、付属のSDカードを本体に入れ、 Print ボタンを押して "Food_Clip_Fast.gcode" を選択すると印刷が始まります。

レベリングがうまく行っていない場合は一段目の印刷がプレートにうまく定着しなくて糸くずのようになるのでその場合はすぐに中止してレベリングをやり直したほうがいいと思います。

出来上がったものがこちらになります。プレートをはがして取り外しました。

テスト印刷の結果

少し糸が伸びてますが、付属のニッパーで切れば特に問題ありませんでした。KP3Sで検索するとZ軸方向の精度が甘いという話が出てきて不安でしたが、今のところ問題なさそうです。（現在売られているTitanなんちゃらというバージョンは以前のものから改良されているらしいのでその辺の事情は変わっているのかもしれません）

3DBenchyの印刷

テストデータの印刷に成功したので、配布されている3Dモデルを印刷する手順を確認するために3DBenchyの印刷を行いました。3DBenchyというのは3Dプリンターのベンチマーク用に設計された船のモデルで、世界で最もプリントされている物体だと言われています。作業はスライサーソフトの導入、KP3Sで3DBency（船）を実際に印刷してみる – ゆるぷとSTLをG-codeに変換 – KINGROON KP3S情報を参考に進めました。

まずは3DBenchyのモデルをダウンロードします。

www.thingiverse.com

"Download All Files"でダウンロードしたファイルを解凍すると"3DBenchy.stl"というファイルが入っています。

次にSTL形式の3Dモデルから実際の印刷に使うG-codeを生成するスライサーというソフトをダウンロードします。いくつか種類があるようですが、無料でユーザーの多いUltimaker Curaを選びました。

ultimaker.com

インストール後最初の起動時にプリンターを聞かれるのでKingroon > KP3Sを選択します。設定を変更したほうがいいという話もありますが、初期設定のままでも大丈夫でした。

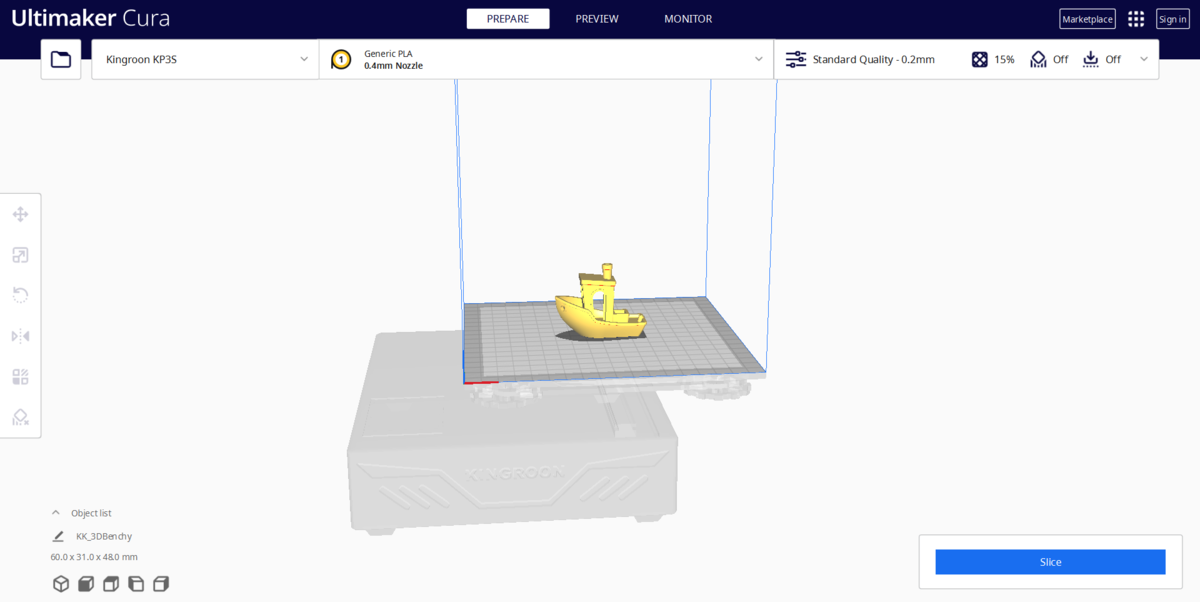
モデルを読み込んだ様子。先人のブログに従って船首が左向きになるよう初期状態から180度回した状態。

右下のSliceボタンを押し、スライス結果をプレビューしたものがこちら。

Slice結果のプレビュー画面

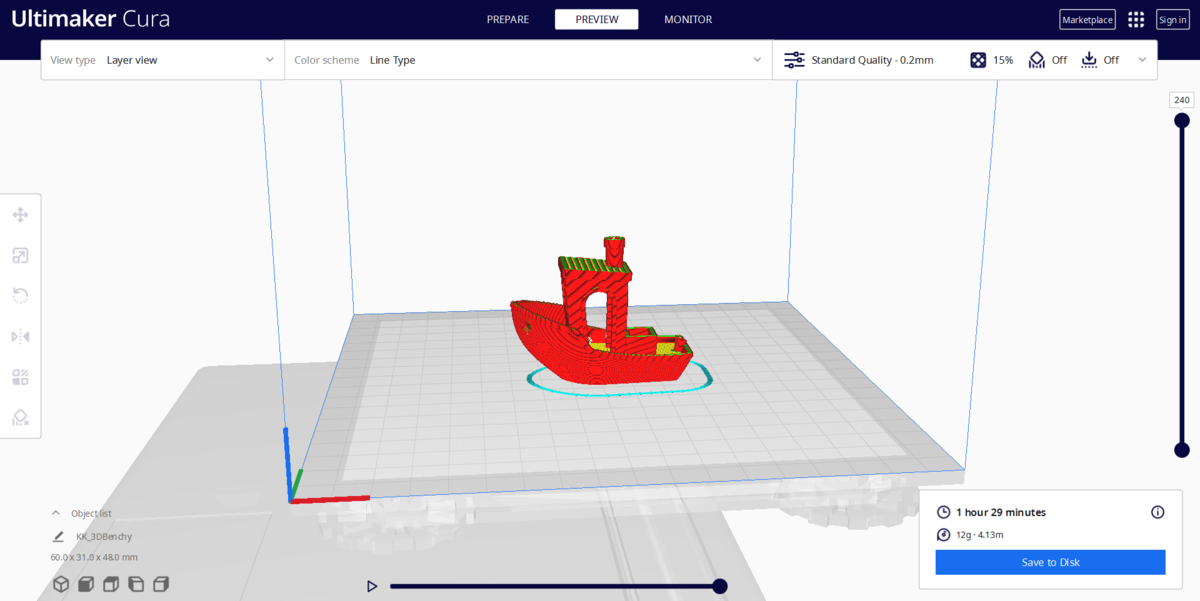
Save To Diskを押してG-codeをDカードに保存したらテストデータと同じように印刷することができます。1時間30分かかりました。

印刷終了直後の状態

横から見た図。積層方式らしいざらつきはあるが十分きれいに印刷できている。

3DBenchyの定性的チェックポイントは船尾のネームプレートの文字が読めないこと以外は大丈夫でした（この項目はhigh-resolution 3D printer向けらしいのでクリアできなくても仕方ないのかもしれない）。定量的チェックポイントも手元の安いノギスで確認できる範囲では問題ありませんでした。

これでワークフローの確認が一通り終わったので、次は自分で設計したモデルを印刷しようと思います。

創作+機械学習 Advent Calendar 2021 結果発表

2021年の年末に創作+機械学習 Advent Calendar 2021というイベントを開催しました。 開始時点での参加者は10人だったのですが、日を追うごとに参加者が増えて最終的には2枚目を作ることになりました。ご参加いただいた皆様、本当にありがとうございました。

kivantium.hateblo.jp

優秀賞の発表

ルールに「2022年1月に参加者の相互投票で優秀賞を決定します」と記載した通り、記事を執筆していただいた方々を対象にして1/1〜1/7の期間で投票を行いました。 2021年内に投稿された23本の記事の中から、良いと思った記事に1人3票投票していていただきました。執筆者22名のうち19名から投票がありました。ご協力ありがとうございました。

得票数上位8つの記事を発表します。

最優秀賞

優秀賞

佳作

最優秀賞には賞金2万円、優秀賞には賞金1万円が授与されます。

審査員特別賞の発表

続いて審査員特別賞です。ルールから審査基準を再掲します。

  • @kivantium賞（機械学習の使い方に新しさを感じる記事を書いた方に授与）
  • @thetenthart賞（創作支援に役立ちそうな記事を書いた方に授与）
  • @xbar_usui賞（機械学習を知らない人でも楽しめる記事を書いた方に授与）

審査員特別賞には賞金5000円が授与されます。各賞に選ばれた記事は次の通りです。

kivantium賞

審査員コメント

音声認識の内部表現から似た音の組を発見して有用な情報を取り出そうとする試みに新しさを感じました。記事に「探したい韻のフレーズを検索する用途に用いるのは必ずしも成功しない」とあり、当初目指していた結果は得られなかったようですが、聞き間違えが生じる仕組みを逆に活用してしまうアイデアの面白さを評価しました。

thetenthart賞

審査員コメント

今回Advent Calendarに参加していただいた皆様ありがとうございます。予想よりも多くの方に投稿していただいて、この分野の潜在的な需要の高さを再認識しました。ハイレベルで興味深い記事が多かった中、多くの方に使ってもらえるツールやデータを公開しているという観点で【2021年】つくよみちゃんと機械学習【音声合成・会話AI】をthetenthart賞に選ばさせていただきました。

つくよみちゃんプロジェクトは、キャラクターの商用フリー化・無料でのコーパス公開・音声合成ソフトの公開など、音声合成に関して多岐にわたる大きな貢献をされていて、これからも音声合成界隈を盛り上げてくださるものだと期待しています。

xbar_usui賞

審査員コメント

今回、どの作品も読み物としても面白かったので、大変に迷いました。 技術的に、あるいはストーリー的に面白いものは他にもあったのですが、多少主観で「このアイデア面白そう！」という目線で選ばせていただきました。

hsjoihsさんの作品は「架空世界の表意文字を手書き認識させる」という非常にメタというか、ある意味ぶっ飛んでいる創作機械学習でちょっとクラクラきました。 まっくすさんの作品は自分で創作した漫画を、さらに海外の人向けに翻訳するために機械学習を用いたというところに魅力を感じました。

他の方々も、大変面白い作品を投稿いただき、ありがとうございました！

f:id:kivantium:20220108221250p:plain:w600
受賞者の皆さま（画像提供: @yumu_7さん）

奨励賞の発表

参加者が想定以上に集まったため、事前に決めていた賞に加えて奨励賞を用意しました。奨励賞に選ばれたのは以下の2つです。

奨励賞には賞金3000円が授与されます。

アンケート結果

投票と同時にアンケートも行ったのでその結果の一部を紹介します。

投票の際に重視した評価基準を教えてください

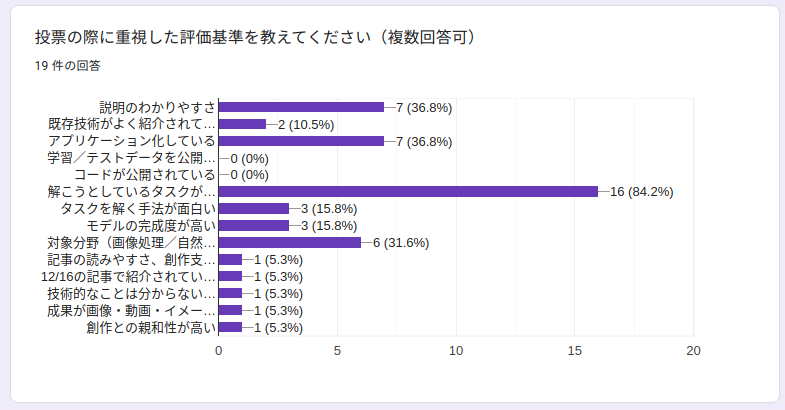
f:id:kivantium:20220108081631p:plain
集計結果

「解こうとしているタスクが面白い (84.2%)」「説明のわかりやすさ (36.8%)」「アプリケーション化している (36.8%)」「対象分野（画像処理／自然言語処理／音声処理など）に興味がある (31.6%)」の順でした。 今年の年末にもAdvent Calendar企画を開催する予定なので、参考にしてください。

今後の活動について

創作機械学習に関連した同人誌を、コミックマーケットや技術書典などの同人誌即売会で出版することを考えています。 現在はアンケートで「とても寄稿したい」を選択した方での執筆を考えておりますが、それ以外にも執筆を望む方がおられましたらTwitter: @thetenthartまでご連絡ください。

内容については基本的に、創作＋機械学習（あるいはデータ分析）に関わる記事各々執筆する方向性で考えていますが、執筆者同士で興味の対象がうまく合えば何か統一的なテーマ（ゲーム創作支援など）でかければ良いかとも思っています。

Discordサーバー 2dmlの宣伝

このAdvent Calenderは2dmlというDiscordサーバーで企画・運営されました。このサーバーでは創作と機械学習に関する情報交換やイベントの開催を行っています。興味がある方は是非ご参加ください。

招待リンク: https://discord.gg/jQNXjkrqGU

また、このAdvent Calendarの読者アンケートを実施しておりますのでご協力お願いします。 創作+機械学習 Advent Calendar 2021 読者アンケート

以上です。創作+機械学習 Advent Calendar 2021 にご参加いただいた皆様ありがとうございました。2022年もよろしくお願いします。